Cu-Mg Example¶
The Cu-Mg binary system is an interesting and simple binary subsystem for light metal alloys. It has been modeled in the literature by Coughanowr et al. [1], Zou and Chang [2] and Zhou et al. [3] and was featured as a case study in Computational Thermodynamics The Calphad Method by Lukas, Fries, & Sundman [4].
Here we will combine density functional theory and experimental calculations of single-phase data to generate a first-principles phase diagram. Then that database will be used as a starting point for a Markov Chain Monte Carlo (MCMC) Bayesian optimization of the parameters to fit zero-phase fraction data.
Input data¶
All of the input data for ESPEI is stored in a public ESPEI-datasets repository on GitHub. The data in this repository is Creative Commons Attribution 4.0 (CC-BY-4.0) licensed and may be used, commercialized or reused freely.
In order to run ESPEI with the data in ESPEI-datasets, you should clone this repository to your computer. Files referred to throughout this tutorial are found in the CU-MG folder. The input files will be very breifly explained in this tutorial so that you are able to know their use. A more detailed description of the files is found on the Gathering input data page.
If you make changes or additions, you are encouraged to share these back to the ESPEI-datasets repository so that others may benefit from this data as you have. You may then add your name to the CONTRIBUTORS file as described in the README.
Phases and CALPHAD models¶
The Cu-Mg system contains five stable phases: Liquid, disordered fcc and hcp, the C15 Laves phase and the CuMg2 phase. All of these phases will be modeled as solution phases, except for CuMg2, which will be represented as a stoichiometric compound. The phase names and corresponding sublattice models are as follows:
LIQUID: (CU, MG)1
FCC_A1: (CU, MG)1 (VA)1
HCP_A3: (CU, MG)1 (VA)1
LAVES_C15: (CU, MG)2 (CU, MG)1
CUMG2: (CU)1 (MG)2
These phase names and sublattice models are described in the JSON file Cu-Mg-input.json file as seen below
{
"components": ["CU", "MG", "VA"],
"refdata": "SGTE91",
"phases": {
"LIQUID" : {
"sublattice_model": [["CU", "MG"]],
"sublattice_site_ratios": [1]
},
"CUMG2": {
"sublattice_model": [["CU"], ["MG"]],
"sublattice_site_ratios": [1, 2]
},
"FCC_A1": {
"sublattice_model": [["CU", "MG"], ["VA"]],
"sublattice_site_ratios": [1, 1]
},
"HCP_A3": {
"sublattice_site_ratios": [1, 0.5],
"sublattice_model": [["CU", "MG"], ["VA"]]
},
"LAVES_C15": {
"sublattice_site_ratios": [2, 1],
"sublattice_model": [["CU", "MG"], ["CU", "MG"]]
}
}
}
Of note is that we will be using the reference state defined by SGTE91.
This reference state is implemented in pycalphad.refdata.
Other reference states can be supported in principle, but must be implemented in pycalphad.refdata.
ESPEI¶
ESPEI has two steps: single-phase fitting and multi-phase fitting. The single-phase fitting step uses experimental and DFT data for derivatives of the Gibbs free energy (\(C_P, H, S\)) for a phase and for the mixing energies within sublattices for each phase to select and fit parameters. The multi-phase fitting uses MCMC to optimize the parameters selected and calculated from the single-phase fitting. These steps can be performed together, or separately. For clarity, we will preform these steps separately. The next two sections are devoted to describing ESPEI’s single-phase fitting and MCMC optimization.
Though it should be no problem for this case, since the data has already been used, you should get in the habit of checking datasets before running ESPEI.
ESPEI has a tool to help find and report problems in your datasets.
This is automatically run when you load the datasets, but will fail on the first error.
Running the following commmand (assuming from here on that you are in the CU-MG folder from ESPEI-datasets):
espei --check-datasets input-data
The benefit of the this approach is that all of the datasets will be checked and reported at once.
If there are any failures, a list of them will be reported with the two main types of errors being JSONError, for which you should read the JSON section of Gathering input data,
or DatasetError, which are related to the validity of your datasets scientifically (maching conditions and values shape, etc.).
The DatasetError messages are designed to be clear, so please open an issue on GitHub if there is any confusion.
First-principles phase diagram¶
In single-phase fittings, parameters are selected using the Akaike information criterion (AIC) to choose an optimal set of parameters from canditate models (here, parameters in Redlich-Kister polynomials) that balance the number of parameters with the goodness of fit. The AIC prevents overfitting or underfitting Gibbs free energy functions with parameterizations with data. The key aspect of this is that ESPEI will avoid overfitting your data and will not add parameters you do not have data for. This is important in the case of structures that should have some temperature dependent contribution to the Gibbs energy parameterization, but the input data only gives 0K formation energies. In this case, temperature dependence cannot be added and calculated to the thermodynamic model. Thus, an abundance of single-phase data is critical to provide enough degrees of freedom in later optimization.
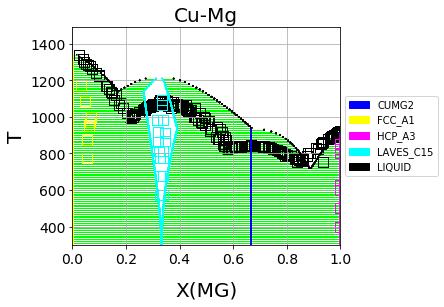
By using the Cu-Mg-input.json phase description for the fit settings and passing all of the input data in the input-data folder, we can first use ESPEI to generate a phase diagram based on single-phase experimental and DFT data.
Currently all of the input datasets must be formation properties, and it can be seen that the formation enthalpies are defined from DFT and experiments for the Laves and CuMg2 phases.
Mixing enthalpies are defined for the for the fcc, hcp, and Laves phases from DFT and for liquid from experimental measurements.
The following command will generate a database named cu-mg_dft.tdb with parameters selected and fit by ESPEI:
espei --input espei-in.yaml
where espei-in.yaml is a ESPEI input file with the following contents
system:
phase_models: Cu-Mg-input.json
datasets: input-data
generate_parameters:
excess_model: linear
ref_state: SGTE91
output:
output_db: cu-mg_dft.tdb
The calculation should be relatively quick, on the order of a minute of runtime.
With the above command, only mininmal output (warnings) will be reported.
You can increase the verbosity to report info messages by setting the output.verbosity key to 1 or debug messages with 2.
With the following code, we can look at the generated phase diagram and compare it to our data.
# First-principles phase diagram
from pycalphad import Database, variables as v
from espei.datasets import load_datasets, recursive_glob
from espei.plot import multiplot
# load the experimental and DFT datasets
datasets = load_datasets(recursive_glob('input-data', '*.json'))
# set up the pycalphad phase diagram calculation
dbf = Database('cu-mg_dft.tdb')
comps = ['CU', 'MG', 'VA']
phases = ['LIQUID', 'FCC_A1', 'HCP_A3', 'CUMG2', 'LAVES_C15']
conds = {v.P: 101325, v.T: (300, 1500, 10), v.X('MG'): (0, 1, 0.01)}
# plot the phase diagram and data
multiplot(dbf, comps, phases, conds, datasets)
Which should result in the following figure
We can see that the phase diagram is already very reasonable compared to the experimental points. The liquidus temperatures and the solubilities of the fcc and Laves phases are the key differences between the equilibrium data and our first-principles phase diagram. The next section will discuss using ESPEI to optimize the parameters selected and calculated based on the single-phase data to these multi-phase equilibria.
MCMC-based Bayesian optimization¶
With the data in the CU-MG input data, ESPEI generated 11 parameters to fit. For systems with more components, solution phases, and input data, may more parameters could be required to describe the thermodynamics of the specific system well. Because they describe Gibbs free energies, parameters in CALPHAD models are highly correlated in both single-phase descriptions and for describing equilibria between phases. For large systems, global numerical optimization of many parameters simultaneously is computationally intractable.
To combat the problem of optimizing many paramters, ESPEI uses MCMC, a stochastic optimzation method. Details of MCMC are better covered elsewhere, such as MacKay’s (free) book: Information Theory, Inference, and Learning Algorithms.
Using MCMC for optimizing CALPHAD models might appear to have several drawbacks. As previously mentioned, the parameters in the models are correlated, but we are also unsure about the shape and size of the posterior distribution for each parameter before fitting. Particularly, traditional Metropolis-Hastings MCMC algorithms require the a prior to be defined for each parameter, which is a problem for parameters in CALPHAD models which vary over more than 6 orders of magnitude.
ESPEI solves these potential problems by using an Ensemble sampler, as introduced by Goodman and Weare [5], rather than the Metropolis-Hastings algorithm. Ensemble samplers have the property of affine invariance, which uses multiple (\(\geq 2 N\) for \(N\) parameters) parallel chains to scale new proposal parameters by linear transforms. These chains, together an ensemble, define a proposal distribution to sample parameters from that is scaled to the magnitude and sensitivity of each parameter. Thus, Ensemble samplers directly address the challenges we expect to encounter with traditional MCMC.
ESPEI uses an Ensemble sampler algorithm by using the emcee package that implements parallelizable ensemble samplers. To use emcee, ESPEI defines the initial ensemble of chains and a function that returns the error as a log-probability. ESPEI defines the error as the mean square error between experimental phase equilibria and the equilibria calculated by the CALPHAD database.
Here, again, it is critical to point out the importance of abundant phase equilibria data. Traditional CALPHAD modeling has involved the modeler participating in tight feedback loops between updates to parameters and the resulting phase diagram. ESPEI departs from this by optimizing just a single scalar error function based on phase equilibria. The implication of this is that if there are phase equilibria that are observed to exist, but they are not in the datasets that are considered by ESPEI, those equilibria cannot be optimized against and may deviate from ‘known’ equilibria.
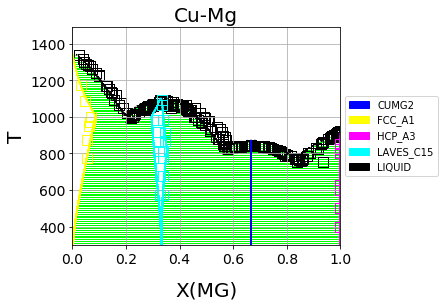
We address this in ESPEI by estimating points for the equilibria. For the Cu-Mg system, it has been experimentally reported that Cu has no solubility in Mg, so there are few measurements of solubility reported in the literature. In order to properly reproduce this and prevent other parameters to be optimized in a way that introduces solubility in the hcp phase, we have added the phase equilibria for the hcp phase (pink squares) to have 100% Mg (0% Cu). These points effectively anchor the hcp phase to have no solubility. Because thermodynamic databases are typically developed for pragmatic reasons, it is sensible to use these estimates, even for more complicated equilibria that there is no data available for. ESPEI allows thermodynamic database to be easily reoptimized with little user interaction, so more data can be added later and the database reoptimized at the cost of only computer time. In fact, the existing database from estimates can be used as a starting point, rather than one directly from first-principles, and the database can simply be modified to match any new data.
Now we will use our zero phase fraction equilibria data to optimize our first-principles database with MCMC.
The following command will take the database we created in the single-phase parameter selection and perform a MCMC optimization, creating a cu-mg_mcmc.tdb:
espei --input espei-in.yaml
where espei-in.yaml is an ESPEI input file with the following structure
system:
phase_models: Cu-Mg-input.json
datasets: input-data
mcmc:
mcmc_steps: 1000
input_db: cu-mg_dft.tdb
output:
output_db: cu-mg_mcmc.tdb
ESPEI defaults to run 1000 iterations and depends on calculating equilibrium in pycalphad several times for each iteration and the optimization is compute-bound. Fortunately, MCMC optimzations are embarrasingly parallel and ESPEI allows for parallelization using dask or with MPI using mpi4py (single-node only at the time of writing - we are working on it).
Note that you may also see messages about convergence failures or about droppping conditions. These refer to failures to calculate the log-probability or in the pycalphad solver’s equilibrium calculation. They are not detrimental to the optimization accuracy, but overall optimization may be slower because those parameter steps will never be accepted (they return a log-probability of \(-\infty\)).
Finally, we can use the newly optimized database to plot the phase diagram
# Optimized phase diagram from ESPEI's multi-phase fitting
from pycalphad import Database, variables as v
from espei.datasets import load_datasets, recursive_glob
from espei.plot import multiplot
# load the experimental and DFT datasets
datasets = load_datasets(recursive_glob('input-data', '*.json'))
# set up the pycalphad phase diagram calculation
dbf = Database('cu-mg_mcmc.tdb')
comps = ['CU', 'MG', 'VA']
phases = ['LIQUID', 'FCC_A1', 'HCP_A3', 'CUMG2', 'LAVES_C15']
conds = {v.P: 101325, v.T: (300, 1500, 10), v.X('MG'): (0, 1, 0.01)}
# plot the phase diagram and data
multiplot(dbf, comps, phases, conds, datasets)
References¶
| [1] | Coughanowr, C. A., Ansara, I., Luoma, R., Hamalainen, M. & Lukas, H. L. Assessment of the Cu-Mg system. Zeitschrift f{ü}r Met. 82, 574–581 (1991). |
| [2] | Zuo, Y. U. E. & Chang, Y. A. Thermodynamic calculation of the Mg-Cu phase diagram. Zeitschrift f{ü}r Met. 84, 662–667 (1993). |
| [3] | Zhou, S. et al. Modeling of Thermodynamic Properties and Phase Equilibria for the Cu-Mg Binary System. J. Phase Equilibria Diffus. 28, 158–166 (2007). doi:10.1007/s11669-007-9022-0 |
| [4] | Lukas, H., Fries, S. G. & Sundman, B. Computational Thermodynamics The Calphad Method. (Cambridge University Press, 2007). doi:10.1017/CBO9780511804137 |
| [5] | Goodman, J. & Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 5, 65–80 (2010). doi:10.2140/camcos.2010.5.65. |
Acknowledgements¶
Credit for initially preparing the datasets goes to Aleksei Egorov.